Least Squares Generative Adversarial Networks Xudong Mao et al. 2016을 바탕으로 작성한 리뷰입니다.
오늘은 GAN, DCGAN에 이어 LSGAN에 대해 리뷰해보겠습니다.
LSGAN은 아이디어가 굉장히 직관적이면서 동시에 까다로운(?) 논문인거 같습니다.
GAN에서 파생되어 나온 모델들이 대부분 그러하듯 LSGAN 또한 GAN의 문제점을 지적하며 개선된 내용을 주장합니다.
1. GAN은 sigmoid cross entropy를 사용하는데, 이는 vanishing gradient problem을 잘 잡지 못한다. LSGAN은 이런 vanishing gradients problem을 해결하였다.
2. GAN의 학습과정이 unstable한데 비해, LSGAN은 stable하다.
3. LSGAN은 상대적으로 high-quality의 이미지를 만들어낸다.
LSGAN이 이러한 성과를 낼 수 있었던건 Least Square를 Loss function에 적용했기 때문입니다.
Least Square은 이름에서도 알 수 있듯이 오차제곱을 최소화 하는것입니다.
아래 그림을 보시며 LS가 어떻게 GAN에 적용되었는지 설명하겠습니다.
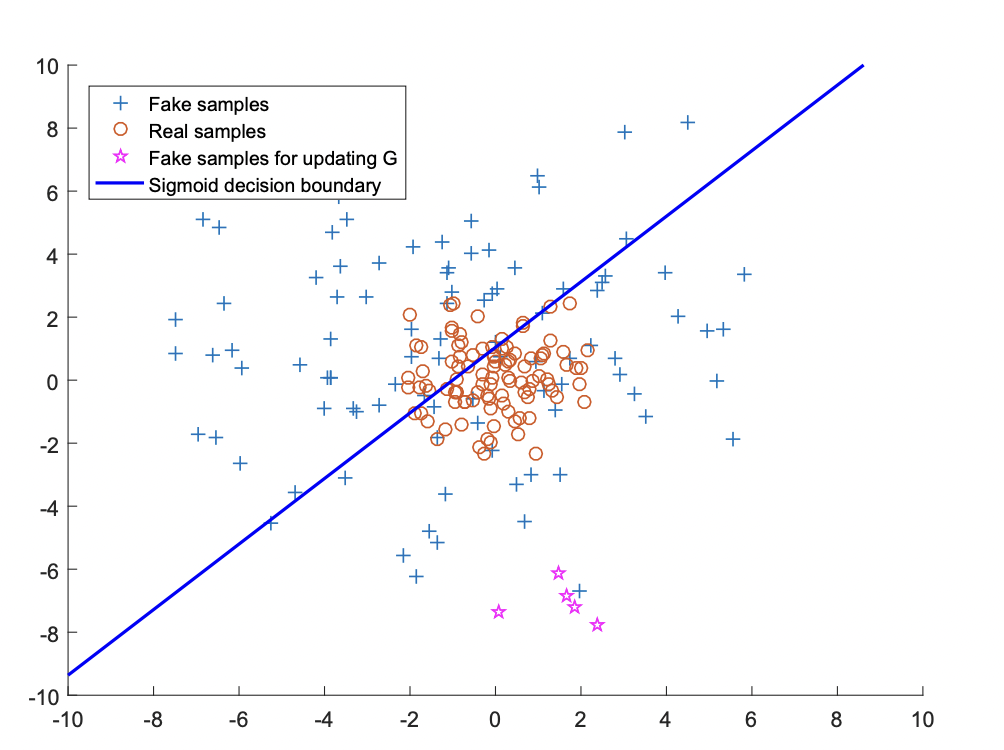
위 그림은 sigmoid cross entropy loss function을 decision boundary(파란선)으로 나타낸 그림입니다.
파란선을 기준으로 위는 가짜 아래는 진짜로 판단합니다. +모양은 가짜data를 나타내고, O는 진짜data를 나타냅니다.
그리고 마지막으로 ☆은 가짜data인데 진짜로 분류된 것들입니다.
☆에 한해서 Generator는 Discriminator를 잘 속이고 있습니다. 하지만 Discriminator를 속였냐가 우리의 최종보스 목표는 아닙니다. 사람이 봤을떄 real data같도록 $p_x$와 최대한 분포가 비슷한 $p_g$를 만드는게 궁극적인 목표라고 할 수 있습니다.
하지만 ☆은 real data O들과 너무 떨어져있습니다. 둘 사이의 거리가 가까워야 분포가 좋아질텐데,,
그래서 적용한것이 Least Square입니다.

이제 Least Square Decision boundary가 추가되었습니다. 이 Decision Boundary가 생김으로써 ☆들은 O와 멀리 떨어져 있을 수록 패널티를 받고 점점 O쪽으로 가까워집니다.
GAN에 Least Square를 적용하면 fake data들이 Discriminator를 속일만큼 정교해지는것은 물론, real data에도 확실히 더 가까워 지겠죠?
여기까지가 LSGAN의 핵심 아이디어에 관한 간략한 설명이었고, 이제 논문의 목차대로 자세하게 내용정리를 해보겠습니다..
Method
1. Regular GANs
$$\underset{G}{min}\underset{D}{max}V_{GAN}(D,G) = E_{x\sim p_{data(x)}}[logD(x)] + E_{z\sim p_{z(z)}}[log(1 - D(G(x)))]$$
Regular GAN의 내용을 잠깐 상기시켜보면 위와 같이 minmax objective을 가졌던것을 기억할 수 있을 것입니다.
2. Least Squares GANs
LSGAN은 Regular GAN의 목적함수에 a-b coding을 추가로 사용합니다.
- $a$ : fake data label
- $b$ : real data label
- $c$ : $G$ 입장에서 $D$가 가짜 데이터를 보고 진짜라고 믿기를 원하는 값
$$\underset{D}{min}V_{LSGAN}(D) = \frac{1}{2}E_{x\sim p_{data(x)}}[(D(x)-b)^2] + \frac{1}{2}E_{z\sim p_{z(z)}}[(D(G(z))-a)^2]$$
$$\underset{G}{min}V_{LSGAN}(G) = \frac{1}{2}E_{z\sim p_{z(z)}}[(D(G(z))-c)^2]$$
min problem들이 최소값이 되기 위해서는 제곱이 되는 값들이 모두 0 이 되어야 합니다.
따라서 $D(x)\rightarrow b$, $D(G(z))\rightarrow a$에 가까워 질수록 값이 작아집니다.
2.1 Benefits of LSGANs
이렇게 Least Square 로 Penalize가 추가된 GAN은, Discriminator의 decision boundary에 안주하지 않고 더 많은 변화량, 즉 gradient를 더 활발하게 생성하기 때문에 vanishing gradients문제를 해소합니다.

loss function의 그래프를 봐도 (a)는 최소로 수렴하는구간이 넓은 반면, (b)는 one point에서 최소값을 갖기 때문에 gradient를 더 활발하게 생성합니다.
2.1 Relations to f-divergence
Regular GAN에서의 증명을 상기시켜보면, GAN의 minmax problem을 풀면 결과적으로 아래와 같이, JSD(pdata || pg)를 최소화하는 식이 나옵니다. ($p_g = p_{data}$, 즉 pg와 data distribution pdata 사이의 괴리를 줄이는 문제와 동치)
$$C(G) = KL(p_{data}\parallel \frac{p_{data}+p_g}{2}) + KL(p_{g}\parallel \frac{p_{data}+p_g}{2}) - log(4)$$
이제, LSGAN이 푸는 문제에도 작은 조건을 추가해보겠습니다.
$$\underset{G}{min}V_{LSGAN}(G) =\frac{1}{2}E_{z\sim p_{z(z)}}[(D(G(z))-c)^2]$$
에 $\frac{1}{2}E_{x\sim p_{data(x)}}[(D(x)-c)^2]$를 추가합니다.
(G가 관여하는 부분이 없기 때문에 더해도 본 solution에는 변화가 없습니다.)
$$\underset{G}{min}V_{LSGAN}(G) = \frac{1}{2}E_{x\sim p_{data(x)}}[(D(x)-c)^2] + \frac{1}{2}E_{z\sim p_{z(z)}}[(D(G(z))-c)^2]\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (a)$$
GAN의 증명에서 증명했듯이, G가 고정되어 있을시에 optimal한 D는 아래와 같이 구할 수 있습니다.
$$D^*(x) = \frac{bp_{data}(x)+ap_g(x)}{p_{data}(x)+p_g(x)}$$
이제 (a)에 $D^*(x)$를 대입하면,
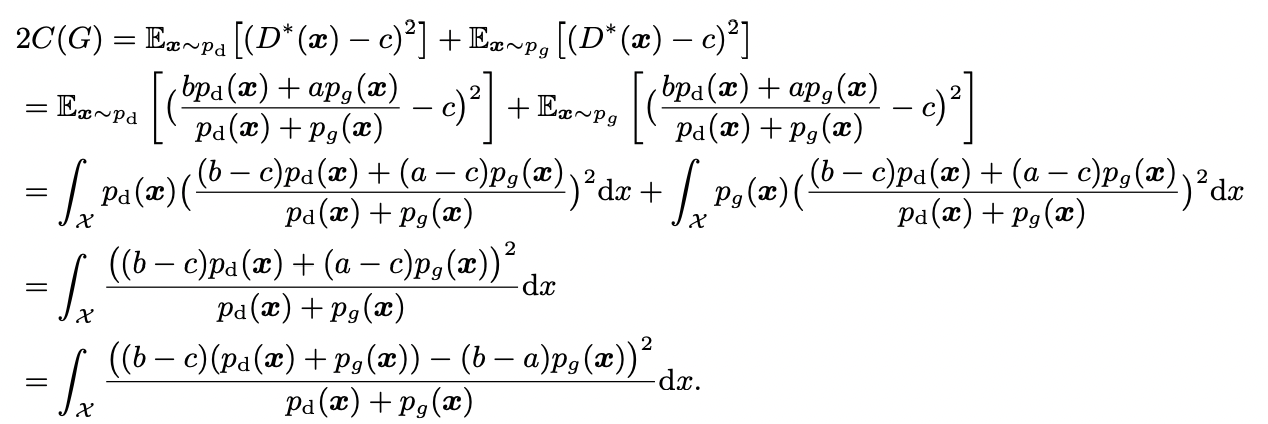
이제 마지막 식에 b-c=1, b-a=2라는 조건을 주게 되면
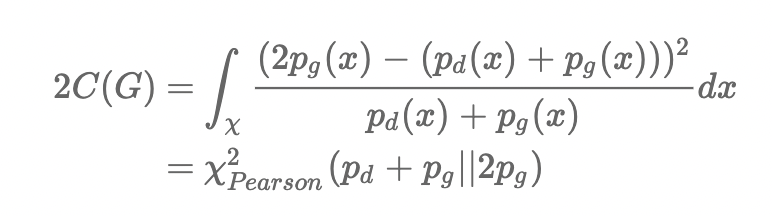
아래와 같이 식이 구해집니다. 결국 LSGAN의 문제는 $p_g + p_d$와 $2p_g$의 $Pearson x^2 divergence$을 최소화 하는것과 동치가 됩니다. 즉 $p_g = p_{data}$가 될때 divergence가 최소가 됩니다.
즉, b-c=1, b-a=2 라는 조건이 주어질때 $Pearson x^2 divergence$를 최소화하는 식이 됩니다.
Experiments and Results

[참고] : http://jaejunyoo.blogspot.com/2017/06/f-gan.html
'Deep Learning > GAN' 카테고리의 다른 글
| [GAN] DCGAN - 논문 리뷰, Paper Review, 설명 (2) (0) | 2021.07.06 |
|---|---|
| [GAN] DCGAN - 논문 리뷰, Paper Review, 설명 (1) (0) | 2021.07.06 |
| [GAN] Generative Adversarial Nets - 증명 (0) | 2021.06.29 |
| [GAN] Generative Adversarial Nets - Paper Review (1) | 2021.06.29 |