딥러닝을 공부하다보면 KL-divergence, JSD-divergence같이 확률분포를 판단하는 척도들을 종종 접하게 된다.
그리고 그런 척도들의 기본이론이 바로 Information Theory, 정보이론이다.
정보량
정보이론의 기본 단위라고도 할 수 있는 정보량은 무엇일까?
정보량 = '깜놀도'
이해를 돕기위해, 여러 비유중에서 '깜놀도'(깜짝 놀라는 정도)라는 비유를 들어서 정리해보겠다.
확률이 매우 낮은 사건이라서 잘 일어나지도 않고, 고로 누적된 데이터도 없는 사건A가있다.
A: 어떤 사람이 로또를 사서 집에가다가 번개를맞고, UFO에 납치됐다가 풀려났는데 아까 산 로또까지 당첨될 사건
A가 일어날 확률 $P(A)$는 $10^{-10000}$보다도 작을것이다. 거의 불가능한 사건이다.
그럼에도 불구하고 사건A가 이런 극악의 확률을 뚫고 발생했다? 놀랄만한 일이다.
깜놀도가 아주 높다. 그리고 A로부터 우리가 얻을 수 있는 정보는 아주 많을것이다.
반대로 확률이 매우 높은 사건 B가 있다.
B: 로또를 샀는데 꽝이 나오는 사건
B가 일어날 확률 $P(B)$ 는 $0.97638469$로 매우 높다. 거의 항상 일어나는 일이라고 봐도 무방하다. 깜짝 놀랄일도 아니고 그냥 겸허히 받아들인다. 따라서 깜놀도가 낮고 새롭게 얻을만한 정보도 별로 없다.
결국 확률이 높을수록 정보량이 낮고,
확률이 낮을수록 정보량이 높은 반비례 관계라고 생각할 수 있다.
이를 수식으로 나타내면 아래와 같다.
$$I(X) = log(\frac{1}{p(x)})$$
$$ = -log(p(x))$$
왜 로그함수를 사용하느냐에 대한 이유에는 2가지가 있다.
1. 로그로 정보에 필요한 최소한의 자원을 표현할 수 있다.
만약 확률이 $\frac{1}{4}$인 사건을 2진수로 표현한다면, $-log_2(\frac{1}{4}) = 2$ 2bit로 표현할 수 있다. → 2는 여기서 필요한 최소한의 자원수이다.
2. log함수의 additive한 성질 때문이다.
독립사건 A, B에 대해, 두 사건이 동시에 일어날 확률은 두 확률값을 곱한 $P(A)P(B)$가 된다. 그리고 그 사건의 정보량 $I(A,B)는 다음과 같이 $I(A) + I(B)$로 쪼개질 수 있다.
$$I(A,B) = -log(P(A)P(B))$$
$$ = -log(P(A)) - log(P(B))$$
$$ = I(A) + I(B)$$
엔트로피
정보량이 단일사건에 대한 정보량이었다면, 엔트로피는 어떤 사건에 대한 확률 분포의 정보량이라고 할 수 있다.
위에서 본 사건 B는 꽝이 당첨되는 사건이었다. 하지만 꽝 외에도 1~5등이 되는 사건이 존재한다. 이제 우리는 꽝에 대한 정보량말고 '로또'자체에 대한 정보량을 볼 것이다.
이때는 각 사건의 정보량 $I(a)$에해당 정보가 등장할 확률$P(a)$를 곱해준다. 이 값을 모두 더하면 정보량의 평균이된다. 엔트로피: H(x)
$$H(x) = E_{P(x)}[I(x)]$$
$$= E_{P(x)}[-logP(x)]$$
$$= \sum_{i=1}^{N}-P(x_i)logP(x_i)$$
즉, 엔트로피는 정보량에 대한 기댓값, 평균이다.
그리고 동시에 사건을 표현하기 위해 요구되는 평균 자원이라고도 할 수 있다.
$log$의 밑에는 다양한 값이 들어올 수 있지만, 아래 상황에서는 2라고 가정한다.
밑을 2로 두면, $-log_2P(x)$는 사건 를 표현하기 위해 필요한 비트수
Example 1.
a,b,c,d로만 이루어진 문자를 이진수로 압축하고 싶다. 각 알파벳의 출현 빈도를 확률로 나타내면 아래와 같다.

이제 엔트로피를 구해보자.
$$H(x) = E_{P(x)}[I(x)]$$
$$= \sum_{i=1}^{4}-P(x_i)logP(x_i)$$
$$=P(a)log(P(a)) + P(b)log(P(b)) + P(c)log(P(c)) + P(d)log(P(d))$$
$$=\frac{1}{2} \times -log_2\frac{1}{2} + \frac{1}{4} \times -log_2\frac{1}{4} + \frac{1}{8} \times -log_2\frac{1}{8} + \frac{1}{8} \times -log_2\frac{1}{8} $$
$$=\frac{1}{2} \times {\color{Red} 1}+ \frac{1}{4} \times {\color{Red} 2} + \frac{1}{8} \times {\color{Red} 3} + \frac{1}{8} \times {\color{Red} 3} $$
$$=1.75$$
엔트로피는 1.75이고 빨간색으로 칠해진 수들은 각사건별로 필요한 비트의 수다.
결과적으로 1.75는 정보를 나타내는데 필요한 최소 평군 자원수다.
a = 0
b = 10
c = 110
d = 111
로 표현할 수 있겠다.
Example 2.
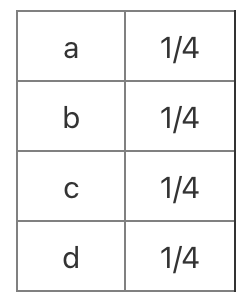
a,b,c,d모두 출현확률이 1/4로 같을땐,
$$=P(a)log(P(a)) + P(b)log(P(b)) + P(c)log(P(c)) + P(d)log(P(d))$$
$$=\frac{1}{4} \times -log_2\frac{1}{4} + \frac{1}{4} \times -log_2\frac{1}{4} + \frac{1}{4} \times -log_2\frac{1}{4} + \frac{1}{4} \times -log_2\frac{1}{4} $$
$$=\frac{1}{4} \times {\color{Red} 2}+ \frac{1}{4} \times {\color{Red} 2} + \frac{1}{4} \times {\color{Red} 2} + \frac{1}{4} \times {\color{Red} 2} $$
$$=2$$
엔트로피는 2, 정보를 나타내는데 필요한 최소 평군 자원수는 2이다.
Example 1과 2를 비교해서 알 수 있는 점은 uniform한 분포일수록 엔트로피(정보량의 평균)이 크다는것이다. Ex1에서는 a가 나올확률이 0.5로 지배적이기 때문에, 비교적 정보량이 낮아지고 예측도 쉬워지지만, 모든 확률이 1/4일경우는 abcd중 뭐가 나올지 예측하기가 오히려 더 힘들어지기 때문에 엔트로피(불확실성)이 커진다.
요약하자면, 엔트로피는 정보량에 대한 기댓값, 불확실성(uncertainty)의 정도도 같은 개념이다.
참고 : 공돌이의 수학정리노트
'Deep Learning > AI수학' 카테고리의 다른 글
| Information Theory 이해하기 - KL Divergence, JSD (0) | 2021.07.14 |
|---|---|
| Information Theory 이해하기 - Cross Entropy (1) | 2021.07.13 |